Page updated:
May 19, 2021
Author: Curtis Mobley
View PDF
Introduction
This page is the first of several on Monte Carlo techniques for solving the Radiative Transfer Equation. As an RTE solution technique, these pages could be considered as Level 2 material under the Radiative Transfer Theory chapter. However, because of the importance of Monte Carlo techniques in a wide range of scientific areas, they warrant a chapter unto themselves.
As used to solve the RTE, Monte Carlo techniques refer to algorithms that use probability theory and random numbers to simulate the fates of numerous photons propagating through a medium. Various averages over ensembles of large numbers of simulated photon trajectories give statistical estimates of radiances, irradiances, and other quantities of interest.
Monte Carlo techniques were developed in the 1940s for studies of neutron transport as needed for the design of nuclear weapons (Metropolis, 1949), (Eckhardt, 1987). The name Monte Carlo was at first a code name for this classified research. The name was well chosen because probability and statistics lie at the heart of both the simulation techniques and the gambling games played at the legendary Monte Carlo Casino in Monaco. Monte Carlo techniques are now highly developed and are used to solve many types of problems in physical and biological sciences; finance, economics, and business; engineering; computer graphics for movie production, and pure mathematics.
An essential feature of Monte Carlo simulation is that the known probability of occurrence of each separate event in a sequence of events is used to estimate the probability of the occurrence of the entire sequence. In the ray-tracing setting, the known probabilities that a light ray will travel a certain distance, be scattered through a certain angle, reflect off on a surface in a certain direction, etc., are used to estimate the probability that a ray emitted from a source at one location will travel through the medium and eventually be recorded by a detector at a different location.
The strengths of Monte Carlo techniques are that
- They are conceptually simple. The methods are based on a straightforward mimicry of nature, which in itself endows them with a certain elegance.
- They are very general. Monte Carlo simulations can be used to solve problems for any geometry (e.g., 3D volumes with imbedded objects), incident lighting, scattering phase functions, etc. It is relatively easy to include polarization and time dependence.
- They are instructive. The solution algorithms highlight the fundamental processes of absorption and scattering, and they make clear the connections between the ray-level and the energy-level formulations of radiative transfer theory.
- They are simple to program. The resulting computer code can be very simple, and the tracing of rays is well suited to parallel processing.
The weaknesses of Monte Carlo techniques are that
- They provide no insight into the underlying mathematical structure of radiative transfer theory. The simulations simply accumulate the results of tracing large numbers of rays, each of which is independent of the others.
- They can be computationally very inefficient. Monte Carlo simulation is a “brute force” technique. If care is not taken, much of the computational time can be expended tracing rays that never contribute to the solution, e.g., because they never intercept a simulated detector.
- They are not well suited for some types of problems. For example, computations of radiance at large optical depths can require unacceptably large amounts of computer time because the number of solar rays penetrating the ocean decreases exponentially with the optical depth. Likewise, the simulation of a point source and a point (or very small) detector is difficult. Monte Carlo techniques are based on tracking individual rays in the geometric optics limit of physical optics and thus cannot address wave phenomena such as diffraction.
This page discusses probability distributions and how they are sampled in Monte Carlo simulations. The next page discusses how light rays are tracked in Monte Carlo simulations. Subsequent pages discuss computational tricks for speeding up calculations and improving the accuracy of the statistical estimates, and the design of Monte Carlo simulations for particular problems. Those pages are placed in Level 2 because of their mathematical nature.
Probability Functions
As a ray travels through a medium, the distance it goes between interactions with the medium, whether it will be absorbed or scattered in a given interaction, the new direction it will travel after a scattering event, etc. are all random variables. In mathematics it is customary to let a capital letter, e.g. , denote a random variable (such as the distance a ray travels) and to let a lower case letter, in this case, denote a value of , e.g. if is distance. Let be any such random variable that is defined over a range of values to . If is distance traveled, and ; if is a polar scattering angle, and or 180 deg, and so on.
The probability density function (pdf) for , denoted , is a non-negative function such that is the probability (a number between 0 and 1) that has a value between and . A pdf must satisfy the normalization
| (1) |
That is, the probability is 1 that will have some value in its allowed domain. The cumulative distribution function (cdf) is a function giving the probability that the random variable will have a numerical value less than or equal to . The cdf is obtained from the corresponding pdf via
Note that a pdf has units of 1/{units of x} and can have a magnitude greater than 1 for some values of , whereas a cdf is nondimensional and grows monotonically from 0 at to 1 at .
The mean or average value of is given by
and the variance of is given by
The pdf for a random variable that can have values only between 0 and 1 is fundamental to Monte Carlo simulation. Let be a random variable drawn from the unit interval between 0 and 1 such that is equally likely to have any value on the interval from 0 to 1. The pdf for is
| (2) |
is said to have a uniform 0 to 1 distribution, denoted by .
We wish to use a randomly drawn value of , which is a known number , to determine a value for a random variable . This is done by regarding going from to as a change of variables. Then the probablity that lies between and is the same as the probability that lies between and . Thus
Because is known from Eq. (2), the left-hand integral can be evaluated to obtain
The fundamental principle of Monte Carlo simulation states that the equation uniquely determines in such a manner that lies in the interval to with probability . That is, drawing a value from a distribution and then solving for gives a randomly determined value of that obeys the pdf for .
The next sections illustrate how this principle is applied for specific examples of determining ray path lengths and scattering angles.
Determining Ray Path Lengths
Recall from the derivation of the RTE that radiance in a particular direction decays due to absorption and scattering out of the beam according to
which integrates to give
where is the beam attenuation coefficient and is the distance from some starting point. In terms of the optical path length this is
This experimentally established exponential decay of radiance can be explained in terms of the fate of individual rays if the probability of any particular ray being absorbed or scattered out of the incident direction between and is
Note that this satisfies the normalization condition (1) with and . The corresponding cdf is . Drawing a random number from a distribution and solving
for gives
Because is also uniformly distributed on , we can just as well use
to determine . Optical distances randomly chosen in this manner, when applied to many rays, are consistent with the exponential decay of radiance with distance traveled. If the water is homogeneous, so that does not depend on , then and the geometric distance a photon travels is given by
Note that the average distance a ray travels is given by
or, for homogeneous water,
The average distance a ray travels between an absorption or scattering interaction with the water is called the mean free path between interactions. Likewise, the standard deviation , which is the square root of the variance , of the optical distance traveled is also 1, or . Thus rays travel on average one optical path length, or meters, but with a large spread of values about that distance.
Determining Scattering Angles
Scattering is an inherently three-dimensional process and must be specified by both polar and azimuthal scattering angles. The scattering phase function can be interpreted as a pdf for scattering from an incident direction to a final direction , per unit of solid angle. If we pick a spherical coordinate system centered on the incident direction and recall the expression for an element of solid angle in spherical coordinates, then we can write
Ocean water is usually well described as isotropic medium, which means that there are no optically preferred directions. (This is not the case, for example, in a cirrus cloud with non-randomly oriented ice crystals.) In that case, the polar and azimuthal scattering angles are independent, and we can write
For an unpolarized beam, the azimuthal angle is equally likely to have any value from 0 to 360 deg, or 0 to radians. Thus the pdf for azimuthal scattering is , the cdf is , and is determined by .
Using this in the previous equation allows us to identify the pdf for the polar angle as
Recall from the discussion of the Volume Scattering Function that phase functions satisfy the normalization
so this function is indeed a pdf. Therefore, to determine the polar scattering angle, we draw a random number as always and solve
| (3) |
for .
In general, Eq. (3) must be solved numerically because of the complicated shape of most phase functions, or when the phase function is defined by tabulated data at a finite number of scattering angles and is fit with a spline (or other) function to generate a continuous function of scattering angle. However, a few commonly used phase functions allow this equation to be solved analytically. The simplest case, isotropic scattering, is instructive.
Isotropic Scattering. The phase function for isotropic scattering is . Substituting this into Eq. (3) leads to
for the determination of the scattering angle. This result may look peculiar until it is remembered that isotropic scattering means that scattering is equally likely into any element of solid angle, not equally likely at every scattering angle . Figure 1 illustrates this important point. Scattering from a collimated beam is simulated two different ways. The scattering events occur at the center of a sphere, and the points plotted on the surface of the sphere show the scattering direction. The arrow at the “north pole” represents the direction of the unscattered beam and a scattering angle of 0. The blue lines are lines of constant scattering angle , with the thick line at the “equator” being deg. In the left panel, the polar scattering angle was drawn from a distribution, i.e., any value of between 0 and 180 deg was equally likely. The right panel drew from the distribution. In both simulations the azimuthal scattering angle was drawn from a distribution. It is visually clear from the left panel that the uniform distribution of values gives too many points near the north pole of the figure, i.e., too many points with scattering angles near 0. The right panel shows an even distribution of points per unit area of the surface of the sphere, i.e., per unit solid angle in any direction.
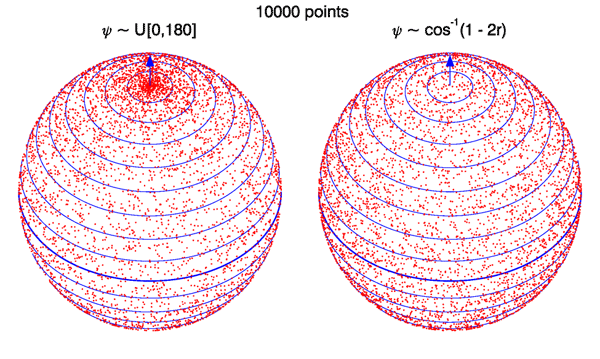
Table 1 displays various phase functions and the formulas obtained from solving used to determine the corresponding scattering angles.
Name | Phase Function | formula |
isotropic | ||
Henyey- |
|
|
Rayleigh |
|
|
cosine or |
if
| |
arbitrary | any
that | must solve |
The widely used Fournier-Forand phase function is
where
Here is the real index of refraction of the particles, is the slope parameter of the hyperbolic distribution, and is evaluated at . This phase function has an analytic cdf (Fournier and Jonasz, 1999)
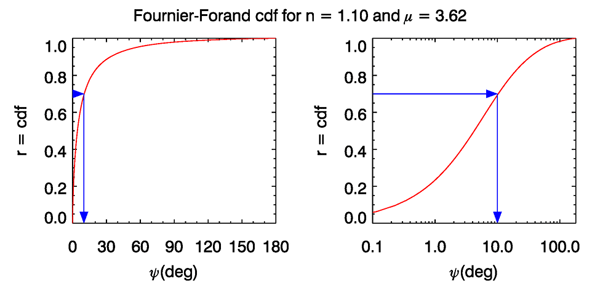
However, solving for (even if possible) would give a formula so complicated that it is numerically more efficient to use Eq. (3) for to build up a table of vs. values for closely spaced values of and the given and parameters, and then to interpolate within this table to obtain values of as values are drawn in the course of a simulation. This is illustrated in Fig. 2, which shows a Fourier-Forand cdf for values of and that give a best fit to the Petzold average particle phase function phase function. The blue arrows show how drawing a value of leads to a scattering angle of about 10 deg. When working with tabulated data for highly peaked phase functions, it is usually adequate to use linear interpolation between the tabulated values.

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.