Page updated:
November 1, 2020
Author: Collin Roesler
View PDF
Measurement of Absorption
From Theory to Reality
Consider a scenario where the goal is to measure the absorption spectrum of a thin layer of material (Figure 1A). The incident radiant power is given by , in the form of a collimated beam. The radiant power transmitted through the layer,, is detected. If , there is no loss of radiant power and therefore no attenuation. If however the medium absorbs some quantity of radiant power, , then , and (Figure 1B). In the case of material that both absorbs and scatters (Figure 1C), the scattered radiant power is given by , and .
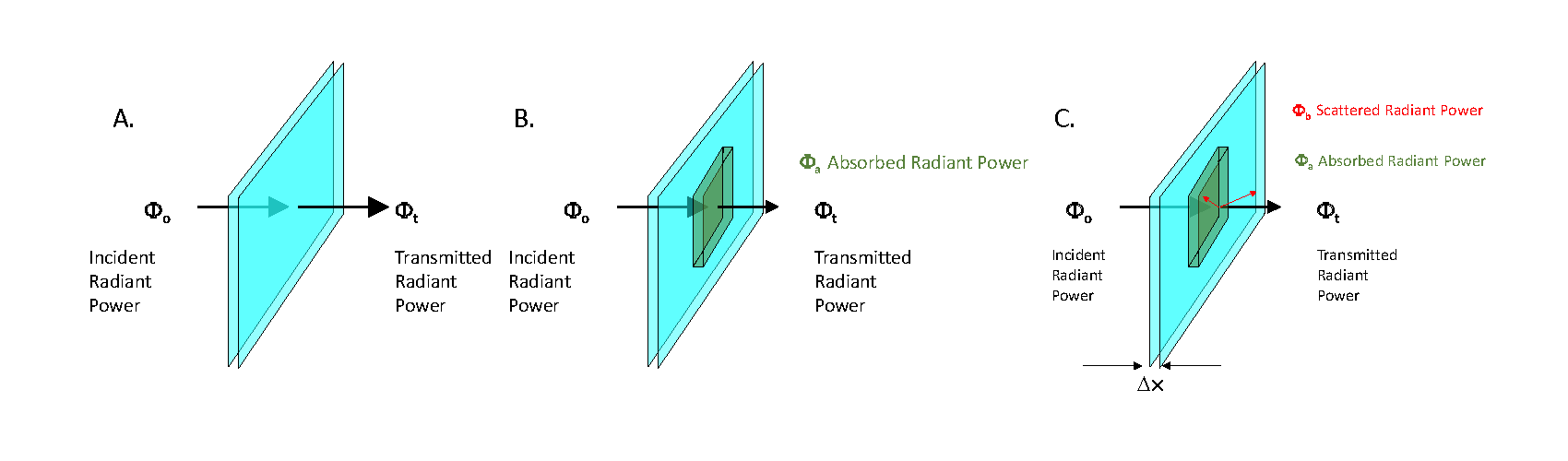
To quantify the absorbed radiant power only, it is necessary to measure both the transmitted and scattered radiant power. This is a requirement for an absorption meter. Consider first a nonscattering material. The measured dimensionless transmittance, , is the fraction of incident power transmitted through the layer:
The absorptance, , is the fraction of incident radiant power that is absorbed ():
The absorption coefficient (with units of ) is the absorptance per unit distance
which, for an infinitesimally thin layer can be expressed as:
Rearranging this expression and taking the limit as yields:
Assuming that the absorption coefficient is constant over the layer of thickness and integrating gives
This equation provides a guide toward designing instruments to accurately measure absorption. The Level 2 pages beginning at Benchtop Spectrometry of Solutions give the specifics on techniques to measure absorption by dissolved and particulate constituents in seawater.

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.