Contents

Page updated: May 19, 2021
Author: Curtis Mobley
View PDF

The Volume Scattering Function (VSF)

We now take into account the angular distribution of the scattered power, with two assumptions. We ﬁrst assume that the medium is isotropic, i.e., its inﬂuence on light is the same in all directions at a given point. This is a reasonable assumption for natural waters in which the particles are randomly oriented by turbulence. We also assume that the incident light is unpolarized. If these two assumptions are true, then the scattering process is azimuthally symmetric. This means that the scattering depends only on the scattering angle $ψ$ , which is measured from the direction of the unscattered beam as shown in Fig. 1. Clearly 0 $\leq ψ \leq π$ .

Figure 1: Geometry used to deﬁne the volume scattering function.

Φ_{i} (λ)

is the incident power onto an area

Δ A

. An amount

Δ Φ_{a} (λ)

of the incident power is absorbed in distance

Δ r

, and

Δ^{2} Φ_{s} (ψ, λ)

is the power scattered into the annular ring of solid angle

Δ Ω

Δ Φ_{t} (λ)

is the transmitted power.

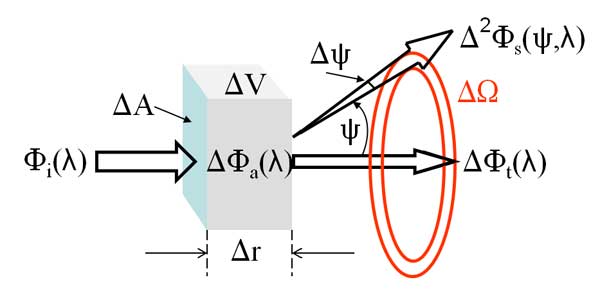
Conceptual Deﬁnition of the Volume Scattering Function

With these two assumptions, the fraction of incident power scattered out of the beam through an angle $ψ$ into a solid angle $Δ Ω$ centered on $ψ$ , is $Δ^{2} Φ_{s} (ψ, λ) ∕ Φ_{i} (λ)$ . The notation $Δ^{2} Φ_{s} (ψ, λ)$ is adopted from ? to indicate that $Δ^{2} Φ_{s} (ψ, λ)$ is a second-order small quantity, that is, it is small because both $Δ r$ and $Δ Ω$ are small. The solid angle $Δ Ω$ now includes all directions within the two red rings shown in the ﬁgure, corresponding to all directions between scattering angles $ψ$ and $ψ + Δ ψ$ . The volume scattering function $β (ψ, λ)$ is deﬁned as the limit of this fraction as $Δ r \to 0$ and $Δ Ω \to 0$ :

β (ψ, λ) \equiv lim_{Δ r \to 0} lim_{Δ Ω \to 0} \frac{Δ^{2} Φ_{s} (ψ, λ)}{Φ_{i} (λ) Δ r Δ Ω} = \frac{1}{Φ_{i} (λ)} \frac{\partial^{2} Φ_{s} (ψ, λ)}{\partial r \partial Ω} (m^{- 1} s r^{- 1}) .

(1)

Recalling the deﬁnition of spectral radiant intensity ?? as scattered power per unit solid angle, the corresponding intensity scattered into the given solid angle $Δ Ω$ is $Δ I_{s} (ψ, λ) = Δ^{2} Φ_{s} (ψ, λ) ∕ Δ Ω$ . Moreover, if the incident power $Φ_{i} (λ)$ falls on an area $Δ A$ , then the corresponding incident irradiance is $E_{i} (λ)$ = $Φ_{i} (λ) ∕ Δ A$ . Noting that $Δ V = Δ r Δ A$ is the volume of water that is illuminated by the incident beam allows Eq. (1) to be rewritten as

β (ψ, λ) = lim_{Δ V \to 0} \frac{Δ I_{s} (ψ, λ)}{E_{i} (λ) Δ V} = \frac{1}{E_{i} (λ)} \frac{\partial I_{s} (ψ, λ)}{\partial V} .

(2)

This form of $β (ψ, λ)$ suggests the name volume scattering function (commonly abbreviated as VSF) and the physical interpretation of scattered intensity per unit incident irradiance per unit volume of water. In the language of a physicist, the VSF also can be interpreted as the diﬀerential scattering cross section per unit volume.

The forms of Eqs. (1) and (2) involving partial derivatives are conceptual deﬁnitions. Instruments that measure the VSF always have to deal with ﬁnite path lengths $Δ r$ and ﬁnite solid angles $Δ Ω$ . The transition from a deﬁnition as a derivative to an instrument design is discussed on Sec. ?? on measuring IOPs.

Scattering Coeﬃcients

Integrating $β (ψ, λ)$ over all directions (solid angles) gives the total scattered power per unit incident irradiance and unit volume of water, in other words the scattering coeﬃcient:

b (λ) = \int_{Ξ} β (ψ, λ) d Ω = 2 π \int_{0}^{π} β (ψ, λ) sin ψ d ψ .

(3)

The $2 π$ in the last equation follows from our assumption that the scattering is azimuthally symmetric about the incident direction. This integration is often divided into forward scattering, 0 $\leq ψ < π ∕ 2$ , and backward scattering, $π ∕ 2 \leq ψ \leq π$ , parts. The corresponding forward and backward scattering coeﬃcients are, respectively,

b_{f} (λ) \equiv 2 π \int_{0}^{π ∕ 2} β (ψ, λ) sin ψ d ψ

(4)

b_{b} (λ) \equiv 2 π \int_{π ∕ 2}^{π} β (ψ, λ) sin ψ d ψ .

(5)

The backscatter fraction, deﬁned by

B_{b} (λ) = {\tilde{b}}_{b} \equiv \frac{b_{b} (λ)}{b (λ)},

(6)

gives the fraction of scattered light that is deﬂected through scattering angles greater than 90 deg. This quantity is fundamental to remote sensing because most of the light leaving the ocean in an upward direction comes from sunlight that was originally heading downward, but which was backscattered into upward directions.

The Scattering Phase Function

The volume scattering phase function¹ , $\tilde{β} (ψ, λ)$ , is deﬁned by

\tilde{β} (ψ, λ) \equiv \frac{β (ψ, λ)}{b (λ)} (s r^{- 1}) .

(7)

Writing the VSF $β (ψ, λ)$ as the product of the scattering coeﬃcient $b (λ)$ times the phase function $\tilde{β} (ψ, λ)$ partitions $β (ψ, λ)$ into a factor giving the magnitude of the total scattering, $b (λ)$ with units of $m^{- 1}$ , and a factor giving the angular distribution of the scattered light, $\tilde{β} (ψ, λ)$ , with units of ${s r}^{- 1}$ . Combining Eqs. (3) and (7) gives the normalization condition for the phase function:

2 π \int_{0}^{π} \tilde{β} (ψ, λ) sin ψ d ψ = 1 .

(8)

This normalization implies that the backscatter fraction can be computed from

B_{b} (λ) \equiv 2 π \int_{π ∕ 2}^{π} \tilde{β} (ψ, λ) sin ψ d ψ .

(9)

The asymmetry parameter g or mean cosine of the phase function is average over all scattering directions of the cosine of the scattering angle $ψ$ , namely

g = ⟨ cos ψ ⟩ \equiv 2 π \int_{0}^{π} \tilde{β} (ψ) cos ψ sin ψ d ψ .

(10)

The asymmetry parameter is a convenient measure of the “shape” of the phase function. For example, if $\tilde{β} (ψ)$ is very large for small $ψ$ , then $g$ is near one. If $\tilde{β} (ψ)$ is symmetric about $ψ$ = 90 degrees , then $g = 0$ . Typical ocean waters have $g$ values in the range of 0.8 to 0.95.

Comment: We have assumed above that the scattering is azimuthally symmetric, so that the directional pattern or angular shape of the VSF depends only on the scattering angle $ψ$ . This is not the case for polarized incident light, even if the medium is isotropic. Thus a linearly polarized laser beam will scatter diﬀerently for diﬀerent azimuthal directions (measured relative to the plane of polarization), even if the medium is isotropic. Description of polarized light requires the Stokes vector formalism and a more complicated description of scattering by polarized light; also see The General Vector RTE.

If the medium contains non-spherical particles that are not randomly oriented, even unpolarized light will scatter diﬀerently for diﬀerent azimuthal directions. This is sometimes the case, for example, in cirrus clouds and ice fogs, which can have non-spherical ice crystals that become oriented in a particular way as the crystals fall through a calm atmosphere. The atmosphere is then an optically anisotropic medium, and scattering is not azimuthally symmetric. Scattering of sunlight in such an atmosphere gives rise to phenomena such as “sun dogs” or parhelia, which are bright spots to either side of the sun.

The Volume Scattering Function (VSF)

Conceptual Deﬁnition of the Volume Scattering Function

Scattering Coeﬃcients

The Scattering Phase Function

Comments for The Volume Scattering Function (VSF):