Effect of Shape on Optical Properties

Emmanuel Boss and Curtis Mobley contributed to this page.

A sphere is not likely to be a good representative of the shape of the average aquatic particle for two main reasons: (1) the majority of marine particles are not spherical, and (2) of all the convex shapes a sphere is rather an extreme shape: for a given particle volume it has the smallest surface-area-to-volume ratio. Only a limited number of studies have examined the IOPs of non-spherical marine particles and results indicate a strong dependence of optical properties, in particular scattering, on shape. See, for example, Kirk (1976), Voss and Fry (1984), Volten et al. (1998), Gordon and Du (2001), MacCallum et al. (2004), Quirantes and Bernard (2004), Quirantes and Bernard (2006), and Gordon (2006).

Methodical evaluation of shape effects on IOPs are presented in two non-peer-reviewed publications, Aas (1984) and Herring (2002); a short book chapter, Jonasz (1987); and in a review by Clavano et al. (2007). Considerably more research has been done on aerosol particles, which are often irregularly shaped mineral particles with high indices of refraction relative to air. Many of those results are pertinent to oceanic particles.

It has been shown in many studies that non-sphericity has its greatest effect in backscatter directions. It is these directions that contribute to the water-leaving radiance, which is the foundation of ocean-color remote sensing. Figure 1 shows a comparison between measured phase functions and those computed by Mie theory for a polydispersion (particle size distribution) of “equivalent” spheres of the same volume. The feature to note in the phase functions is that Mie theory gives values that differ by as much as a factor of three in backscatter directions.

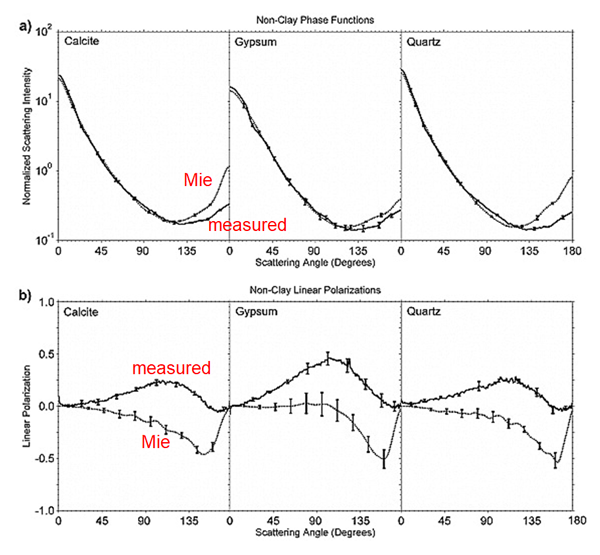
Figure 2 shows another comparison of spherical and randomly oriented non-spherical particles. These phase functions were computed using the equivalent of Mie theory for prolate (“football” shaped) and oblate (“pancake” shaped) spheroids (Asano and Yamamoto (1975)). In the figure insets, $a∕b$ is the ratio of the semimajor ($a$) and semiminor ($b$) axes of the spheroid, $\alpha =2\pi a∕\lambda$ is the size parameter computed using the semimajor axis, and $\tilde{m}$ is the particle index of refraction relative the the surrounding medium. The values for a sphere ($a∕b=1$) were computed using a sphere with the same area as the spheroid. At small scattering angles ($\psi \lesssim 20deg$), shape has a minimal effect, but the sphere versus oblate spheroid phase functions are an order of magnitude different at backscatter directions.

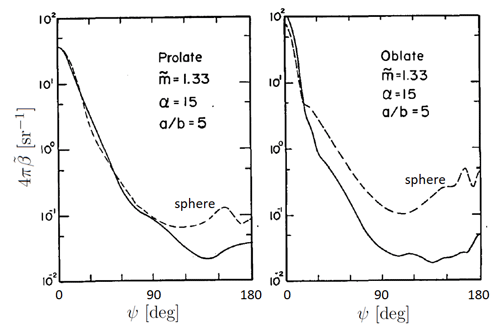
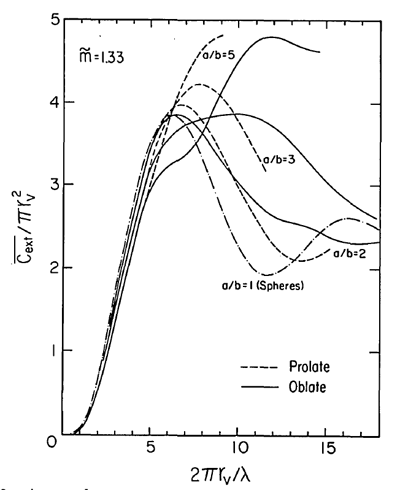
Figure 3 shows orientation-averaged extinction cross sections ($\overline{C_{ext}}$) normalized by the particle area computed using the radius $r_v$ of the volume-equivalent sphere, as a function of the size parameter computed using $r_v$. For small particles, the shape has minimal effect, but for size parameters of order 10, there is a factor-of-two difference in the normalized extinction cross sections.

One of the applications of in-water optical measurements is the inversion of measured volume scattering functions (VSFs) to obtain particle size distributions. The underlying physics is that diffraction accounts for much of the light scattered through small angles, $\psi \lesssim 10$ or 20 deg. To first order, the amount of diffracted power is proportional to the cross sectional area of the particle “seen” by the incident beam. The scattered power is fairly insensitive to the particle composition or index of refraction. Small particles scatter (diffract) more power into large scattering angles; large particles diffract more power into very small angles. Thus a measurement of the VSF between, $\psi \approx 0.1$ deg and 10 or 20 deg can be inverted to get an estimate of the particle area size distribution of the scattering particles. Converting the area PSD to a volume PSD requires an assumption about the shape of the particles in the form of a median diameter for the particles in each region of the area PSD. For details see Agrawal and Pottsmith (2000) or the November 1991 issue Applied Optics (vol. 30, No. 33), which was a special issue on optical particle sizing.

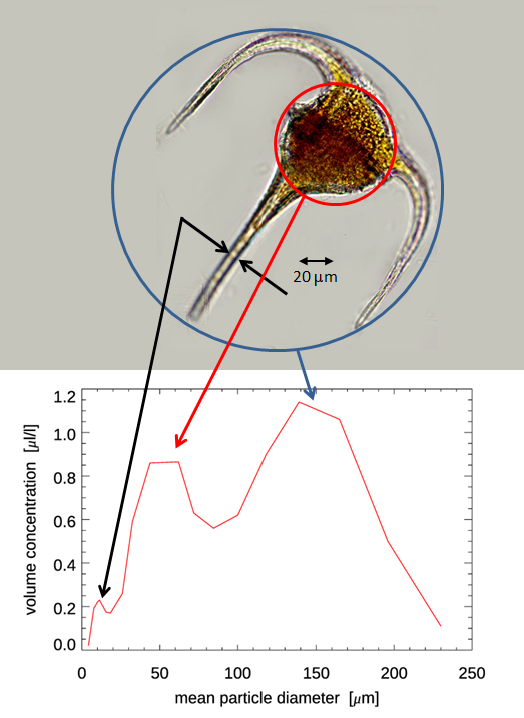
The bottom panel of Fig. 4 shows a PSD retrieved from a culture of the dynoflagellate Ceratium longipes using the LISST-100 instrument (Sequoia Scientific, Inc.). From just the PSD, it would be reasonable to conclude that the culture contained a mixture of small, $\sim 10\mu m$; medium, $\sim 50\mu m$; and large, $\sim 150\mu m$ sized particles. The top panel of the figure shows a photograph of an actual Ceratium longipes. It is seen that there is a central body with long, narrow spines. The LISST was “seeing” the narrow spines, the central body, and the overall size of the phytoplankton. This is actually a quite remarkable retrieval and shows the power of the instrument for resolving objects of various sizes. This figure should be sufficient to convinced you of the futility of trying to define an “equivalent spherical particle” for use in Mie theory when a particle has such a complex shape.

The preceding figures are sufficient to make the point that non-spherical particles can have much different scattering properties than spheres, and that using a volume- or area-equivalent sphere in Mie calculations can give results much different from the actual non-spherical particles. It is difficult to generalize about the optical properties of non-spherical particles because their shapes can be so different: spheroids, long-chain diatoms, plate-like mineral liths, fractal aggregates, etc. In addition to shape effects defined by the boundary of the particle, phytoplankton have shape effects due to their non-homogeneous internal structure as defined by chloroplasts, gas vacuoles, and cell walls.

However, a few results can be summarized as follows:

• For particles much smaller than the wavelength of light, the inherent optical properties of non-spherical particles are similar to those of spheres with the same volume.
• For randomly oriented convex particles much larger than the wavelength of light (the geometric optics limit) the absorption, scattering and attenuation are similar to those of spheres with a similar average cross-sectional areas.
• In general, however, about the only safe thing to say is that non-spherical particles often have IOPs that differ by a factor of two, and sometimes by a factor of ten, from what would be obtained by Mie theory using equivalent-volume or equivalent-area spheres.

There exist numerical techniques for computation of the optical properties of non-spherical particles. The two most commonly used are the T-matrix method and the Discrete Dipole Approximation (DDA). These techniques are extremely mathematical and computationally intensive, and can require extensive effort just to define the problem. The DDA, for example, divides the particle into many very small volume elements, each of which then scatters as a dipole when the incident electromagnetic radiation induces a dipole moment in the volume element. However, you must first define the size and shape of the particle. Publicly available codes for these techniques may come with a gallery of pre-defined shapes such as spheroids, disks, or cylinders, but for more irregular shapes, you must first “build in” the particle shape, which can be a laborious process. In addition, the computatioins may be limited in the range of size parameters that can be computed. The best source for finding such codes, in a variety of computer languages, is SCATTERLIB.