Lambertian BRDFs

Actual measurements of BRDFs of ocean bottom materials like sand or sea grass canopies have rarely been made, although some measurements of sediments do exist (e.g., Zhang et al. (2003)). Because of the lack of measurements and models of the BRDF for actual ocean bottom materials, it is usually assumed that a bottom is a Lambertian reﬂecting surface.

A Lambertian surface by deﬁnition reﬂects radiance equally into all directions. Its BRDF is simply

B R D F_{L a m b} (𝜃_{i}, ϕ_{i}, 𝜃_{r}, ϕ_{r}) = \frac{ρ}{π},

(1)

where $ρ$ is called the reﬂectivity of the surface. The reﬂectivity varies from zero for a completely absorbing (“black”) surface, to one for a completely reﬂecting (“white”) surface. There are no Lambertian surfaces in nature, but matte paper is good approximation except at grazing angles $(𝜃_{i}$ and $𝜃_{r}$ near 90 degrees), where the surface begins to look “shiny.”

There is sometimes confusion as to how Lambertian surfaces reﬂect light. You will sometimes see a statement like

A Lambertian surface reﬂects light equally into all directions. Lambertian surfaces therefore are also called isotropic/uniform/perfectly diﬀuse reﬂectors.

You can also see statements like

A Lambertian surface reﬂects light with a cosine angular distribution. Lambertian surfaces therefore are also called cosine reﬂectors.

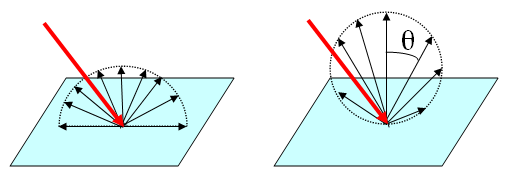
These statements conjure up diﬀerent mental images, as shown in Fig. 1, and appear to be contradictory.

Figure 1: The mental images corresponding to the two descriptions of Lambertian surfaces.

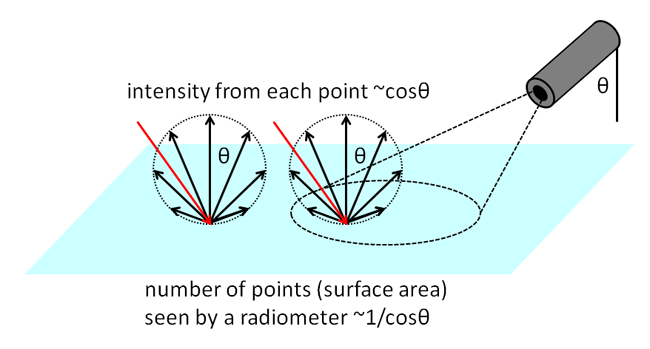
However, either statement can be correct or incorrect, depending on which measure of light is used. Each point of a Lambertian surface reﬂects intensity in a cosine pattern, as in the right-hand panel of Fig. 1, which is the correct form of the second statement. However, when the surface is viewed with a radiometer with a ﬁnite ﬁeld of view, the area of the surface seen by the radiometer is proportional to $1 ∕ cos 𝜃$ . The radiance measured comes from the the intensity reﬂected from each point $(\propto cos 𝜃)$ times the number of points seen $(\propto 1 ∕ cos 𝜃)$ , and is therefore independent of $𝜃$ . Thus the measured reﬂected radiance is independent of the viewing direction, which corresponds to the ﬁrst statement. This is illustrated in Fig. 2.

Figure 2: Resolution of the paradoxical statements about how Lambertian surfaces reﬂect light.

In addition to their mathematical simplicity, Lambertian surfaces have an extremely important property. To see what it is, compute the irradiance reﬂectance $R = E_{u} ∕ E_{d}$ of a Lambertian surface (here we use d and u subscripts to identify the downwelling and upwelling irradiances, respectively, as is common in optical oceanography, but we’ll keep the i and r subscripts in the integrals):

\begin{align} R = & \frac{E_{u}}{E_{d}} = \frac{\iint_{2 π_{r}} L_{r} (𝜃_{r}, ϕ_{r}) | cos 𝜃_{r} | d Ω_{r}}{\iint_{2 π_{i}} L_{i} (𝜃_{i}, ϕ_{i}) | cos 𝜃_{i} | d Ω_{i}} \\ = & \frac{\iint_{2 π_{r}} [\iint_{2 π_{i}} L_{i} (𝜃_{i}, ϕ_{i}) B R D F (𝜃_{i}, ϕ_{i}, 𝜃_{r}, ϕ_{r}) | cos 𝜃_{i} | d Ω_{i}] | cos 𝜃_{r} | d Ω_{r}}{\int \int_{2 π_{i}} L_{i} (𝜃_{i}, ϕ_{i}) | cos 𝜃_{i} | d Ω_{i}} & (2) \end{align}

The ﬁrst equation here is just the deﬁnitions of the plane irradiances in terms of the incident (downwelling) and reﬂected (upwelling) radiances. The diﬀerential of solid angle is $d Ω = sin 𝜃 d 𝜃 d ϕ$ , and the double integrals are over the corresponding hemispheres of $2 π s r$ . In going to the second equation, Eq. (3) of the BRDF page has been used to write the upwelling radiance reﬂected from the surface in terms of the downwelling radiance onto the surface and the BRDF of the surface. Equation (2) is completely general and is the fundamental equation for computing the irradiance reﬂectance of any surface, given the BRDF of the surface and the incident radiance onto the surface.

Substituting the Lambertian BRDF of Eq. (1) into Eq. (2) and rearranging gives

R = \frac{\frac{ρ}{π} [\iint_{2 π_{i}} L_{i} (𝜃_{i}, ϕ_{i}) | cos 𝜃_{i} | d Ω_{i}] \iint_{2 π_{r}} | cos 𝜃_{r} | d Ω_{r}}{\iint_{2 π_{i}} L_{i} (𝜃_{i}, ϕ_{i}) | cos 𝜃_{i} | d Ω_{i}} = ρ,

since the integrals over $2 π_{i}$ cancel, and the integral over $2 π_{r}$ equals $π$ . A Lambertian surface thus has the property that its irradiance reﬂectance $R$ equals its reﬂectivity $ρ$ and, furthermore, its irradiance reﬂectance $R$ is independent of the incident radiance. Both of these results are true only for Lambertian surfaces. For non-Lambertian surfaces, $R$ generally depends both on the surface and on the incident lighting, as seen in Eq. (2).

Fortunately, the use of a Lambertian BRDF for ocean bottom materials in radiative transfer calculations usually results in errors of less than 10 per cent (and often less) in predicted upwelling radiances as viewed for near-nadir directions (the geometry for most remote sensing), so long as the reﬂectivity $ρ$ of the assumed Lambertian surface equals the irradiance reﬂectance $R$ of the actual non-Lambertian surface. Thus the crucial measurement to make is the irradiance reﬂectance of the bottom for the incident lighting conditions of interest (Mobley et al., 2003).

Lambertian BRDFs

Comments for Lambertian BRDFs: