An Analytical Asymptotic Solution for Internal Sources

As already noted, exact pencil-and-paper solutions of the radiative transfer equation are extremely rare, but there are a few. Here is an interesting one related to bioluminescence.

Consider an infinitely deep ocean with homogeneous IOPs and a uniform distribution of bioluminescing material. The material is isotropically emitting with a source function $S\left(z,𝜃,\varphi ,\lambda \right)=S_{o}W{m}^{-3}s{r}^{-1}n{m}^{-1}$ at some wavelength. What is the spectral radiance deep within this ocean?

The RTE for this problem is (dropping the wavelength $\lambda$)

Because the source is directionally isotropic, the radiance also should be independent of direction when the depth is sufficiently far from the surface boundary. Because the source is constant with depth, the radiance should not depend on the depth when far from the surface boundary. Thus $L\left(z,𝜃,\varphi \right)\to L_o$, a constant value, at great depth. The left side of the RTE is then zero, and the radiance can be taken out of the path integration. The RTE then becomes

The integral of the volume scattering function over all directions (all scattering angles) is by definition the scattering coefficient $b$. Thus the RTE reduces to just

which gives the radiance as

where $a=c-b$ is the absorption coefficient. This is the same asymptotic solution as was derived with the assumption of no scattering in the discussion of exact analytical solutions of the RTE. Here we see that this simple solution holds for any volume scattering function.

This analytic solution is easily tested with HydroLight. A run was done using $a=1m^{-1},b=4m^{-1}$, and a Petzold “average particle” phase function for the water IOPs. The sun was placed at a 50 deg zenith angle in an otherwise black sky; the solar irradiance onto the level sea surface was $E_d=1W{m}^{-2}n{m}^{-1}$. The source magnitude was $S_o=0.1W{m}^{-3}s{r}^{-1}n{m}^{-1}$. Figure 1 shows the radiance as a function of depth and direction looking upward to see the downwelling radiance $L_d$ (green), looking downward at the upwelling radiance $L_u$ (purple), and looking horizontally toward (blue), at perpendicular to (red), and away from (orange) the Sun’s azimuthal direction.

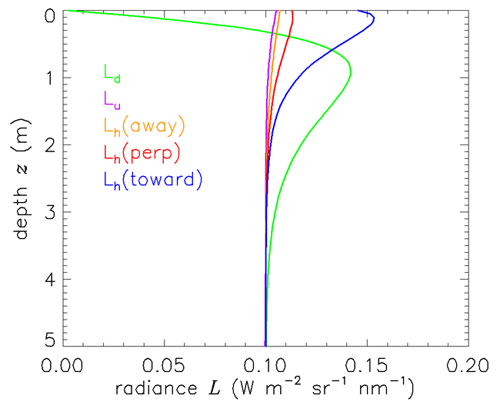
Figure 2 shows the radiances when an isotropic phase function is used, and all other simulation conditions remain the same. The near-surface radiances are now different. In particular, the three horizontal directions are all identical because of the isotropic scattering. However, the radiance at depth remains the same.

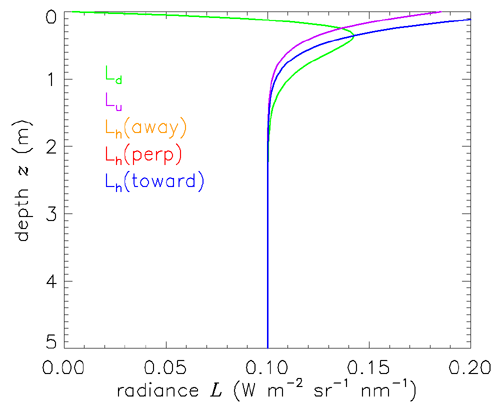
Thus the radiance does depend on depth and direction near the sea surface, where transmitted sky radiance contributes significantly to the total. However, within a few meters (about 20 optical depths for these IOPs) of this boundary, all radiances converge to the predicted value of $L_o=S_o∕a=0.1W{m}^{-2}s{r}^{-1}n{m}^{-1}$. Although the rate of approach to the final radiance value depends on the scattering phase function, sun and sky conditions, and sea state, the solution far from the surface boundary does not.

Depending on your point of view, this simulation can be taken as a numerical confirmation that the analytic solution is correct, or as a validation of the HydroLight code by comparison with a known solution of the RTE.