Blackbody Radiation

The birth date of modern physics can be regarded as December 14, 1900, when Max Planck presented his derivation of the spectral distribution of radiant energy in thermodynamic equilibrium with matter at a given temperature. The derivation of this distribution is both conceptually and mathematically subtle, and Max well deserved his subsequent Nobel Prize. Planck’s function is commonly called the blackbody radiation spectrum.

As derived in most physics books (e.g., Liboff (1980), Chapter 2; or Eisberg and Resnick (1985), Chapter 1), Planck’s function is expressed as a spectral energy density:

where $\nu$ is frequency in $s^{-1}$, $h=6.62607015\cdot 10^{-34}Js$ is Planck’s constant, $c=2.99792458\cdot 10^{8}m{s}^{-1}$ is the speed of light in vacuo, $k=1.380649\cdot 10^{-23}J{K}^{-1}$ is Boltzmann’s constant, and $T$ is the temperature in Kelvin. $U_E\left(\nu \right)$ thus has units of $J∕\left(m^3{s}^{-1}\right)=J∕\left(m^{3}Hz\right)$, or energy per unit volume per unit frequency interval (with frequency measured in Hertz = cycles per second).

For ease of comparison with the Sun’s irradiance, or with the irradiance measured at the entrance of a blackbody cavity, Eq. (1) can be converted to spectral plane irradiance as a function of wavelength. The energy contained in a unit frequency interval $d\nu$ must equal the energy contained in the corresponding wavelength interval $d\lambda$, i.e.,

Recalling that $\nu =c∕\lambda$ gives $d\nu =-\left(c∕{\lambda }^2\right)d\lambda$, and Eq. (1) becomes

which has units of has units of $J∕\left(m^{3}m\right)$, or energy per unit volume per unit wavelength interval (with wavelength measured in meters).

The scalar irradiance $E_o$ is related to the energy density by $E_o=Uc$. One way to see this is to think of the many photons making up the energy density. How many photons “hit” a small spherical detector per unit time, there to be recorded as scalar irradiance, equals how many photons there are times how fast they are moving, i.e. $E_o=Uc$. Radiation in thermodynamic equilibrium is isotropic and unpolarized. For isotropic radiance, $E_o=4E_d$, where $E_d$ is the plane irradiance. Thus Eq. (2) can be converted to spectral plane irradiance by a factor of $c∕4$:

This is the form of Planck’s law seen, for example, in Leighton (1959), page 65.

Two final transformations of Eq. (3) are needed for comparison with the Sun’s solar irradiance as measured at the top of the earth’s atmosphere, as seen in Figs. (1) and (2) of the next page on light from the Sun. First, in accordance with the $r^2$ law for irradiance, the irradiance emitted at the Sun’s surface (presumed to be a blackbody in the present discussion) is reduced by a factor of ${\left(R_{\text{Sun}}∕R_{\text{Earth}}\right)}^2$ to obtain the irradiance at the mean distance of the earth’s orbit. Here $R_{\text{Earth}}=1.496\cdot 10^{8}km$ is the radius of the Earth’s orbit, and $R_{\text{Sun}}=6.95\cdot 10^{5}km$ is the Sun’s radius. Finally, a factor of $10^{-9}$ is applied to Eq. (3) to convert the wavelength spectral interval from meters to nanometers. The resulting equation is

where $E_d\left(\lambda \right)$ is now in $W{m}^{-2}n{m}^{-1}$, although the wavelength is still measured in meters on the right-hand side of the equation for consistency with the SI units for $h,c$ and $k$.

Integrating Eq. (3) over all wavelengths gives the total plane irradiance emitted by a black body:

where $\sigma =\left(2{\pi }^5{k}^4\right)∕\left(15h^3{c}^2\right)=5.6703\cdot 10^{-8}W{m}^{-2}{K}^{-4}$ is the Stefan-Boltzmann constant. The Sun’s total (over all wavelengths) irradiance as measured at the top of the atmosphere is approximately $1368W{m}^{-2}$. Carrying this value back to the Sun’s surface via a factor of ${\left(R_{\text{Earth}}∕R_{\text{Sun}}\right)}^2$ and inserting the result into Eq. (5) gives a corresponding black body temperature of $T=5,782K$. That is, a black body at this temperature emits the same total irradiance as does the Sun. This temperature is then used in Eq. (4) to generate the blackbody spectra seen in the figures of the Light from the Sun page.

Other forms of the blackbody spectrum are sometimes useful. As already noted, blackbody radiation is isotropic. For isotropic radiance $L_o$, $E_d=\pi L_o$, where $\pi$ has units of steradian. Thus formula (3) for plane irradiance can be converted to a formula for blackbody radiance $L_{BB}$ by dividing by $\pi$:

For some applications it is useful to know the photon density or photon irradiance. The photon density $U_Q$ is obtained from the energy density by dividing the energy density $U_E$ by the energy $h\nu$ of a single photon. Thus Eq. (1) gives

where $U_Q$ has units of $photons∕\left(m^{3}Hz\right)$. Similarly, Eq. (3) can be divided by the energy per photon in wavelength units, $hc∕\lambda$, to obtain the photon plane irradiance

where $Q_d$ has units of $photons∕\left(s{m}^{2}m\right)$. Integrating this equation over all wavelengths gives the total number of photons emitted per second per unit area by a blackbody:

where ${\sigma }_Q=\left(4.808\pi k^3\right)∕\left(h^3{c}^2\right)=1.520\cdot 10^{15}photons{s}^{-1}{m}^{-2}{K}^{-3}$ is the photon equivalent of the Stefan-Boltzmann constant. Thus the total energy emitted by a blackbody is proportional to $T^4$, but the total number of photons emitted is proportional to $T^3$. As the temperature increases, the blackbody spectrum shifts toward the blue, and relatively fewer more-energetic short-wavelength photons are needed to keep up with the increasing energy output.

It is also common to use wavenumber $\tilde{\nu }=1∕\lambda$ as the spectral variable. A change of variables based on $U_E\left(\nu \right)\left|d\tilde{\nu }\right|=U_E\left(\lambda \right)\left|d\lambda \right|$ and $d\lambda ∕d\tilde{\nu }=-{\lambda }^2$ then gives

which has units of $J∕\left(m^3{m}^{-1}\right)$, or energy per unit volume per unit wavenumber interval (with wavenumber measured in 1/meters). Other formulas in terms of wavenumber are obtained as before.

Table 1 summarizes various formulas for blackbody radiation. These cover everything needed for optical oceanography. However, the Spectral Calculations website has much additional information about blackbody radiation, including such esoterica as how the spectrum shifts if the blackbody source is moving at relativistic speeds.

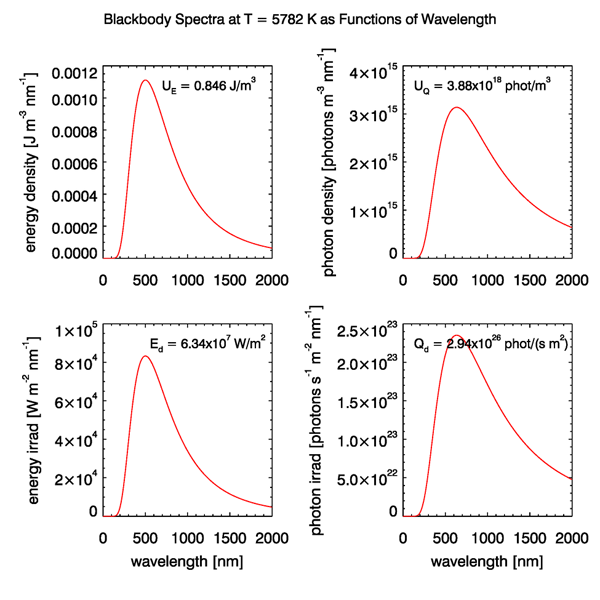
Figure 1 shows the energy and photon densities, and energy and photon irradiances, for a temperature of $T=5782K$, corresponding approximately to the Sun’s surface temperature. These curves were computed using the first four formulas in Table 1. It should be noted that the energy spectra have their maxima at about 500 nm for this temperature, whereas the photon spectra have their maxima at about 635 nm. That is, where the Sun’s output is a maximum depends on what measure of the output is used, as well as on which variable is used for the spectral density. This important matter is discussed further on the page A Common Misconception.