Measurement of Absorption

From Theory to Reality

Consider a scenario where the goal is to measure the absorption spectrum of a thin layer of material (Figure 1A). The incident radiant power is given by ${\Phi }_o$, in the form of a collimated beam. The radiant power transmitted through the layer,${\Phi }_t$, is detected. If ${\Phi }_t={\Phi }_o$, there is no loss of radiant power and therefore no attenuation. If however the medium absorbs some quantity of radiant power, ${\Phi }_a$, then ${\Phi }_t<{\Phi }_o$, and ${\Phi }_o={\Phi }_t+{\Phi }_a$ (Figure 1B). In the case of material that both absorbs and scatters (Figure 1C), the scattered radiant power is given by ${\Phi }_b$, and ${\Phi }_o={\Phi }_t+{\Phi }_a+{\Phi }_b$.

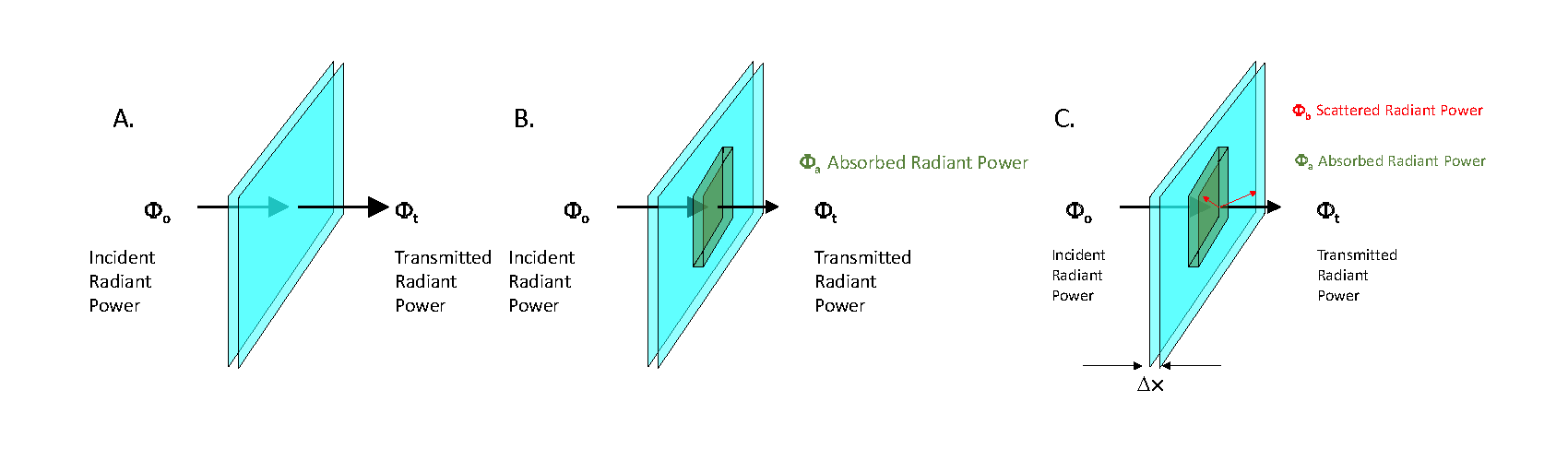
To quantify the absorbed radiant power only, it is necessary to measure both the transmitted and scattered radiant power. This is a requirement for an absorption meter. Consider first a nonscattering material. The measured dimensionless transmittance, $T$, is the fraction of incident power transmitted through the layer:

The absorptance, $A$, is the fraction of incident radiant power that is absorbed ($1-T$):

The absorption coefficient $a$ (with units of $m^{-1}$) is the absorptance per unit distance

which, for an infinitesimally thin layer can be expressed as:

Rearranging this expression and taking the limit as $\Delta x\to 0$ yields:

Assuming that the absorption coefficient is constant over the layer of thickness $x$ and integrating gives

This equation provides a guide toward designing instruments to accurately measure absorption. The Level 2 pages beginning at Benchtop Spectrometry of Solutions give the specifics on techniques to measure absorption by dissolved and particulate constituents in seawater.