Page updated:
February 13, 2021
Author: Curtis Mobley
View PDF
Whitecaps
The contribution of white caps and foam to the TOA radiance depends on two factors: the reflectance of whitecaps per se and the fraction of the sea surface that is covered by whitecaps.
Following Gordon and Wang (1994b), the contribution of whitecaps and foam at the TOA is
where is the diffuse atmospheric transmission in the viewing direction, is the diffuse transmission in the Sun’s direction, and is the non-dimensional normalized whitecap reflectance. is defined in the same manner as was the normalized water-leaving reflectance in Eq. (3.3) of the Normalized Reflectances page, namely
| (1) |
where is the whitecap radiance. It is assumed that the whitecaps are Lambertian reflectors, so that (unlike for ) does not depend on direction . This gives the interpretation (Gordon and Wang (1994b), page 7754) that ” is the reflectance–the reflected irradiance divided by the incident irradiance–that a Lambertian target held horizontally at the TOA would have to have to produce the radiance .” can be interpreted as the average reflectance of the sea surface that results from whitecaps in the absence of atmospheric attenuation.
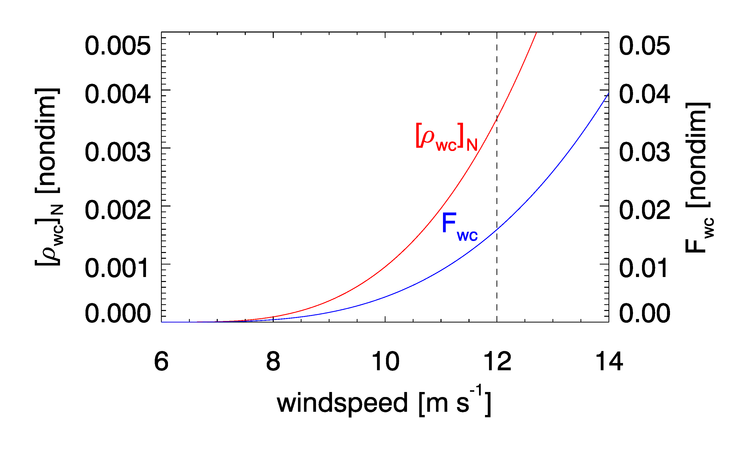
The effective whitecap irradiance reflectance is taken from Koepke (1984) to be 0.22 (albeit with error bars). This reflectance is independent of wavelength. This gives , where is the fraction of the sea surface that is covered by whitecaps. The fractional coverage is taken from Stramska and Petelski (2003), who give two models for for :
where is the wind speed in at 10 m. Formula (3) for undeveloped seas is used on the assumption that if the seas are well developed it is probably stormy, hence cloudy, so that remote sensing is not possible. The blue curve in Fig. (4) shows for undeveloped seas.
The final model for is then taken to be
A whitecap correction is applied for wind speeds in the range . The factor is a normalized whitecap reflectance that describes the decrease in reflectance at red and NIR wavelengths. This factor is taken from Figs. 3 and 4 of Frouin et al. (1996); the values are
| = | 412 | 443 | 490 | 510 | 555 | 670 | 765 | 865 |
| = | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0.889 | 0.760 | 0.645 |
Linear interpolation is used as needed between these values. Figure 1 shows the whitecap reflectance as given by Eq. (4) when .

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.