Contents

Page updated: May 19, 2021
Author: Curtis Mobley
View PDF

The Secchi Disk

Father Angelo Secchi, S. J., seen in Fig. 1, was primarily an astronomer and spectrocopist, but he also made signiﬁcant contributions to meteorology and several other ﬁelds. Among his many accomplishments, he pioneered the use of spectroscopy as a way to classify stars by their spectal type, he was the ﬁrst to realize that the Sun is a star, and he was the ﬁrst to use maps of atmospheric pressure as an aid to weather forecasting. He had only one publication in oceanography, in 1865, but it was a good one. Pitarch (2020) gives a nice overview of Secchi’s oceanographic work.

Figure 1: Angelo Secchi, 1818-1878.

A Secchi disk is a white disk, typically 30 cm in diameter (in oceanographic applications), weighted and attached to a cord marked with the distance from the disk. The disk is lowered into the water and observed as it goes deeper and deeper, as seen in Fig. 2. The depth at which it disappears from view is the Secchi depth, $z_{S D}$ . The Secchi depth gives an easily obtained measure of water transparency. However, there are many sources of variability in this measurement. Sky light reﬂected by the water surface can reduce the visibility (hence a dependence on solar zenith angle and sky conditions), as do waves on the surface, which tend to break up the image of the disk as seen from above the surface. The disk will be easier to see when well illuminated on a bright day than near twilight. Finally, this is one of the few measurements still made in science where the human eye is an integral part of the measurement. Thus if you have better vision that I have, you may be able to see the disk deeper than I can. In spite of all of these uncertainties, the Secchi depth is surprisingly reproducible for diﬀerent environmental conditions and observers, so it is useful for some purposes. There is also a large historical database of Secchi disk readings going back to the days of sailing ships (e.g., World Ocean Database), so proper interpretation of Secchi depths may even be useful for studies of long-term changes in ocean waters.

Figure 2: A Secchi disk being lowered into greenish water. Photo by R. Kirby from The Secchi Disk Study.

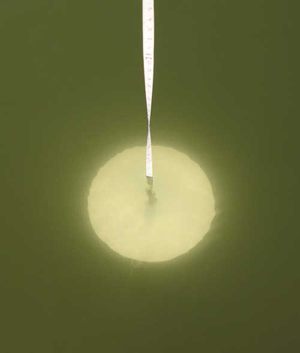
The previous pages on photometry give the background needed to derive the maximum depth at which a Secchi disk can be seen.

The Classical Secchi Depth Model of Preisendorfer

Consider only the case of looking straight down, and drop the direction arguments in luminances and contrasts, e.g. $L_{v B} (z, \hat{ξ}) = L_{v B} (z)$ . The underlying idea is that a disk at some depth $z$ is illuminated by the downwelling plane illuminance $E_{d v} (z)$ . The luminance reﬂected by the disk then propagates upward to the observer as a narrow beam of luminance. The development then proceeds as follows.

The downwelling plane illuminance at depth $z$ is given by

E_{d v} (z) = E_{d v} (0) exp [- {⟨ K_{d v} ⟩}_{z} z],

(1)

where ${⟨ \dots ⟩}_{z}$ denotes the average over 0 to $z$ .

The target is assumed to be a Lambertian reﬂector with an illuminance reﬂectance of $R_{v T}$ . The luminance reﬂected by the target is then

L_{v T} (z) = E_{d v} (z) R_{v T} ∕ π .

(2)

The backgound water is also assumed to be a Lambertian reﬂector, so that

R_{v B} (z) = \frac{E_{u v} (z)}{E_{d v} (z)} .

(3)

The luminance of the background water is then

L_{v B} (z) = E_{d v} (z) R_{v B} (z) ∕ π .

(4)

The inherent contrast at depth $z$ is

\begin{align} C_{i n} (z) = & \frac{L_{v T} (z) - L_{v B} (z)}{L_{v B} (z)} \\ = & \frac{R_{v T} - R_{v B} (z)}{R_{v B} (z)} & (5) \end{align}

where the last equation follows from (2) and (4) into (5).

The apparent contrast of the Secchi disk as seen from just below the sea surface is

C_{a p} (0) = \frac{L_{v T} (0) - L_{v B} (0)}{L_{v B} (0)}

(6)

(Note that in this development the argument 0 refers to depth $z$ , not to the distance from the target, which is $z$ .)

The luminance diﬀerence law

L_{v T} (0) - L_{B v} (0) = [L_{v T} (z) - L_{v} (z)] exp [- {⟨ c_{v} ⟩}_{z} z]

(7)

allows the apparent contrast to be written as

C_{a p} (0) = \frac{[L_{v T} (z) - L_{v B} (z)]}{L_{v B} (0)} exp [- {⟨ c_{v} ⟩}_{z} z]

(8)

by (7) into (6).

Inserting (2) and (4) into (8) then gives

C_{a p} (0) = \frac{R_{v T} - R_{v B} (z)}{R_{v B} (0)} \frac{E_{d v} (z)}{E_{d v} (0)} exp [- {⟨ c_{v} ⟩}_{z} z]

(9)

Assuming that $R_{v B} (0) = R_{v B} (z)$ and using (1) and (5) gives

C_{a p} (0) = C_{i n} (z) exp [- ({⟨ K_{d v} ⟩}_{z} + {⟨ c_{v} ⟩}_{z}) z]

(10)

This equation gives the apparent contrast of the Secchi disk as seen from just below the water surface. For viewing from above the surface, we must account for loss of contrast caused by the water surface. This loss is due both to refraction by waves and to surface-reﬂected sky light. Thus

C_{a p} (a i r) = 𝒯 C_{a p} (0) = 𝒯 C_{i n} (z) exp [- ({⟨ K_{d v} ⟩}_{z} + {⟨ c_{v} ⟩}_{z}) z]

where $𝒯$ denotes the transmission of contrast, not of luminance or illuminance.

The Secchi depth $z_{S D}$ is the depth at which the apparent contrast in air falls below a threshhold contrast $C_{T}$ . Solving for $z_{S D}$ when $C_{a p} (a i r) = C_{T}$ gives

\begin{align} z_{S D} = & \frac{ln [\frac{𝒯 C_{i n} (z)}{C_{T}}]}{{⟨ K_{d v} ⟩}_{z_{S D}} + {⟨ c_{v} ⟩}_{z_{S D}}} & (11) \\ \equiv & \frac{Γ}{{⟨ K_{d v} ⟩}_{z_{S D}} + {⟨ c_{v} ⟩}_{z_{S D}}} . & (12) \end{align}

Studies with human observers show that $C_{T}$ depends on the angular subtense of the disk and on the ambient luminance (e.g., Table 1 of Preisendorfer (1986)). The values of $Γ$ vary from about 6 to 9 for a disk with $R_{v T} = 0.85$ , depending on the water reﬂectance $R_{v B}$ (which is 0.015 to 0.1; Table 2 of Preisendorfer (1986)). The HydroLight code uses $Γ = 8$ as its default.

Note that Eq. (12) must be solved interatively because ${⟨ K_{d v} ⟩}_{z_{S D}}$ and ${⟨ c_{v} ⟩}_{z_{S D}}$ are averages over the (unknown) Secchi depth $z_{S D}$ . This is easily done after solution of the radiative transfer equation to some depth greater than $z_{S D}$ over the visible wavelengths. The photopic $K_{d v} (z)$ and $c_{v} (z)$ can then be computed from $E_{d} (z, λ)$ and $c (z, λ)$ . The values of $K_{d v}$ and $c_{v}$ just below the water surface (at depth 0) are then used to get an initial estimate of $z_{S D}$ , which is then used to compute an improved estimate of the depth-averaged $K_{d v}$ and $c_{v}$ , and so on. Convergence is obtained within a few iterations.

The Secchi Depth Model of Lee et al.

Preisendorfer’s analysis does not consider variability in $z_{SD}$ due to factors like the disk diameter or the solar zenith angle. Therefore,Lee et al. (2015) re-examined the classic theory of the Secchi disk. They assumed that

The disk needs not be angularly small and can perturb the ambient light ﬁeld seen near the edge of the disk.
Visibility is not based on target vs background luminance diﬀerences at the sharp edge of the disk, but on on diﬀerences in target and background reﬂectances.
Visibility is determined by the wavelength where the disk is most visible (which can change with depth and between water bodies), rather than on broadband photopic variables.

They argue that the classic analysis should

Replace the photopic $K_{d v} (z)$ with $K_{d} (z, λ_{m i n})$ , where $λ_{m i n}$ is the wavelength at which $K_{d} (z, λ)$ is a minimum; and
Replace the photopic $c_{v} (z)$ with $1.5 K_{d} (z, λ_{m i n})$ .

One end result of their analysis is a formula of the form (Eq. 28 of their paper)

z_{S D} = \frac{γ}{2.5 K_{d} (z, λ_{m i n})},

(13)

where $γ$ depends on a diﬀerence in reﬂectances, rather than on contrasts as seen in Eq. (11). This formula has the great virtue that $K_{d} (z, λ_{m i n})$ can be estimated from multi- or hyperspectral satellite imagery.

Comparison of $z_{S D}$ measured and computed by Eq. (13) gives reasonable agreement (see Fig. 6 of their paper). However, comparison of Lee et al. $z_{S D}$ predictions with those of the classic theory have not been made.

Black-and-White Secchi Disks

Secchi himself, and oceanographers ever since, used an all-white disk, usually 30 cm in diameter (Secchi also measured the depths at which colored disks disappeared). However, limnologists almost always use a black-and-white disk, usually 20 cm in diameter. An example is seen in Fig. 3. The use of a disk with black and white quadrants traces back to a civil engineer, G. C. Whipple, who described such a disk in a book published in 1899 (G. C. Whipple, The Microscopy of Drinking Water, John Wylie and Sons, page 115). This “Whipple disk” then became the standard for work in fresh water. There seems to be no good reason to pick an all-white versus a black-and-white disk. A qualitative argument has been made that the black quadrants give a “standard reference” for comparison with the white quadrants when used in shallow water that may be aﬀected by bottom reﬂectance (but if bottom reﬂectance is detectable, the Secchi depth is probably deeper than the bottom and a measurement cannot be made). Although Hou et al. (2007) give a rigorous analysis of why a Secchi disk disappears based on spatial frequencies of the imaged disk, they treat only the all-white disk.

Given that oceanographers and limnologists generally live in diﬀerent worlds and never speak to each other, I have never seen a comparison of Secchi depth measured by all-white and black-and-white disks employed at the same time in the same water.

Figure 3: A black-and-white Secchi disk as used in limnology.

See comments posted for this page and leave your own.

Comments for The Secchi Disk:

Loading Conversation

« Contrast