Page updated:
March 13, 2021
Author: Curtis Mobley
View PDF
A Classic IOP Model for Case 1 Water
This page presents an early model for the IOPs of Case 1 water. It is based on a reformulation by Morel and Maritorena (2001) of earlier work by Prieur and Sathyendranath (1981) and Gordon and Morel (1983). This is the model seen in Eqs. (3.27) and (3.40) of Light and Water (1994). This IOP model is presented here for historical purposes and is retained in HydroLight for comparison purposes, where it is called the “Classic Case 1” IOP model in the user interface.
Absorption
The absorption coefficient is modeled as the sum of three components:
| (1) |
where is the absorption by pure water, is the absorption by chlorophyll-bearing particles (phytoplankton) and co-varying detritus, and is the absorption by co-varying colored dissolved organic matter (CDOM).
Absorption and scattering by water are discussed on the Water page.
Absorption by particles
The particle absorption is modeled by
| (2) |
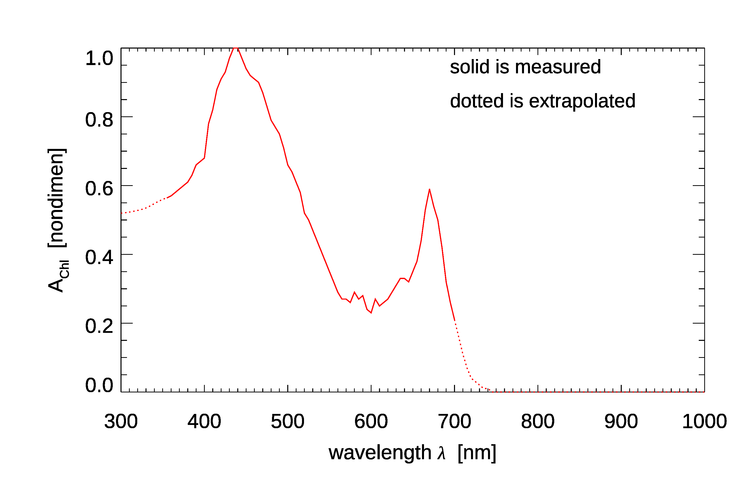
where is the chlorophyll concentration profile in , and is the non-dimensional chlorophyll-specific absorption coefficient given in Prieur and Sathyendranath (1981) (their ) and in Morel (1988) (his Fig 10c), as extrapolated to 300 and 1000 nm. This is shown in Fig. 1. It should be noted that this is independent of the chlorophyll concentration. Thus only the magnitude of the particle absorption coefficient depends on ; the shape of the spectrum is the same for all values. The original data covered 350-700 nm. Extrapolation of the original to 300 and 1000 nm was done by eye and is somewhat uncertain, especially for the UV wavelengths; see the discussion of absorption near 300 nm on the New Case 1 IOP Model page.
Absorption by Colored Dissolved Organic Matter
CDOM absorption is assumed to covary with particle absorption according to
| (3) |
Thus the CDOM absorption at 440 nm is assumed to be 20% of the particulate absorption at 440 nm. This proportionality constant is an average of many measurements, as is the 0.014 wavelength slope factor. In a particular water body the both of these values can be different.
Note that the absorption model of Eqs. (1-3) reduces to that of pure water if . This is slightly different than some formulations (e.g., Morel and Maritorena (2001), their Eq. 16-18), which include a small amount of background CDOM absorption even in the absence of phytoplankton. The inclusion of a small amount of background CDOM is reasonable, but in all honesty, the residual was removed from the equations as used in HydroLight because I just got tired of explaining to HydroLight users why they didnt get exactly the same results as for pure water when they plugged in in the Case 1 IOP model. In any case, the difference is negligible except at extremely low Chl values, in which case the model is suspect anyway.
Scattering
CDOM is assumed to be non-scattering.
The scattering coefficient for the particles is modeled by
| (4) |
where the defaults are , and .
The user of this IOP model must specify both the chlorophyll concentration and the scattering phase function for the particles. One way to specify the particle phase function is to give the particle backscatter fraction, , and then use a Fournier-Forand phase function with the requested value of , as described in Mobley, et al. (2002).
Various formulas for as a function of chlorophyll can be found in the literature. For example, Ulloa et al. (1994) give an empirical formula for at 550 nm in Case 1 waters,
| (5) |
and Twardowski et al. (2001) present another formula,
| (6) |
Such formulas for can be used for rough guidance in specifying the phase function in the absence of other information about the phase function. However, it must be remembered that scattering in general, and in particular, correlates poorly with , and there can be order-of-magnitude variability in the measured value of among different data sets for a given .
The particle backscatter fraction can chosen to be the same at every wavelength, or be a function of wavelength according to the power law
| (7) |
As with all IOP models, this model may give good values on average, but can be considerably in error when applied to a specific water body. In any case, the use of the New Case 1 IOP Model is recommended for general use, especially near 300 nm.

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.