Scattering Overview

Curtis Mobley and Emmanuel Boss contributed to this page.

When light interacts with matter one of three things can occur:

Absorption:: The light can disappear, with its radiant energy being converted into other forms, such as the energy of a chemical bond or heat.
Elastic Scattering:: The light can change direction, without a change of wavelength.
Inelastic Scattering:: The light can undergo a change of wavelength, usually to a longer wavelength, and usually in a diﬀerent direction.

The ﬁrst of these processes is described in the Absorption Chapter beginning at Absorption Overview. This page begins the chapter on scattering, which refers to any change of direction and/or wavelength of light.

Why is Scattering Important?

If you are interested in phytoplankton physiology, absorbed light is all that matters. Light absorbed by phytoplankton provides the energy that drives photosynthesis; light elastically scattered by phytoplankton has no eﬀect on photosynthesis and is not of interest to a plankton biologist. Therefore many more papers have been published on absorption by phytoplankton than on scattering by phytoplankton. Similarly, it is only the light that is absorbed by water molecules that heats water. Parameterizations of upper-ocean heating rates often use Gershun’s Law to compute how much light is absorbed and turned into heat without explicit consideration of scattering.

However, both absorption and scattering are equally important to the prediction and understanding of light propagation.

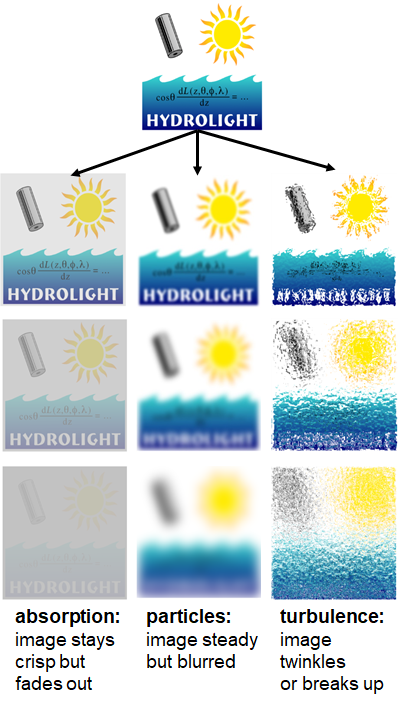
Both absorption and scattering aﬀect visibility in ways that are illustrated in Fig. 1. Absorption removes light from a beam and thus makes a distant image darker. Scattering through small angles blurs the edges of an image, and can cause other eﬀects such as twinkling or mirages, which aﬀect the appearance of distant objects. Visibilty is discussed in detail in the Photometry and Visibility Chapter beginning at Visibility Introduction.

Figure 1: Illustration of absorption and scattering eﬀects on visibility.

Ocean-color remote sensing essentially measures light leaving the oceans to determine how absorption in the water column changed sunlight in what was measured. The measured light comes from scattering within the water column—from either backscattering at angles greater than 90 degrees or from multiple forward scattering at angles of a few tens of degrees or greater. Without scattering there would be no remote sensing of the oceans to understand how absorption has modiﬁed the in-water light ﬁeld. To be more speciﬁc, without elastic scattering, downwelling sunlight would continue to head downward into the ocean depths, eventually to be absorbed. The ocean would appear a dim red color due to chlorophyll ﬂuorescence. Without inelastic scatter, the ocean would be black because there would be no Raman scatter or ﬂuorescence to create even a small amount of upwelling light.

Scattering also enhances the eﬀect of absorption. If light is scattered many times, the distance traveled by a light ray in going from depth $z_{1}$ to depth $z_{2}$ is greater than just the straight-line geometric distance that would be traveled by the initial ray. This gives the light a greater chance of being absorbed before reaching $z_{2}$ . Hence the saying, “A little bit of absorption goes a long ways if you have a lot of scattering.”

Any interaction of light with matter can cause a change in direction or wavelength. It does not matter whether the change in direction comes from reﬂection or refraction by a surface (such as sunlight reﬂected or transmitted by the sea surface), from reﬂection or refraction by a particle that is much larger than the wavelength of light, or from the light’s propagating electric ﬁeld causing electrons in an atom or molecule to oscillate and radiate light into all directions. Although you will sometimes see terms like “surface scattering” (for reﬂection by a surface) or “volume scattering” (for interactions within a volume of water), these process are all scattering and are all caused by essentially the same underlying physics, as discussed on the Physics of Scattering page.

The left panel of Fig. 2 shows what the world looks like with scattering. The right panel of the ﬁgure shows what the same scene would look like without scattering. In the left panel, the bright light near the Sun (the Sun’s aureole) results from small-angle scattering by atmospheric particles. The halo is caused by light being refracted through hexagonal ice crystals in the cirrus clouds. The blue sky comes from light being scattered through large angles by atmospheric gases (mostly nitrogen and oxygen molecules). The view of the land comes from sunlight being reﬂected by the surfaces of the rock and ice. Without scattering, the only light seen would be the Sun’s unscattered direct beam reduced by a small amount of atmospheric absorption, as seen in the right panel of the ﬁgure.

Figure 2: Left panel: A spectacular scene taken from Annapurna South Base Camp in Nepal. Right panel: what the same scene would look like without scattering. Photo by Anton Yankovyi from Wikimedia, reproduced under the Wikimedia Commons license.

Deﬁnitions

This section reviews the quantities commonly used to describe scattering. For additional discussion, see the page on Inherent Optical Properties and several following pages.

The volume scattering function (VSF), $β ({\hat{ξ}}^{'} \to \hat{ξ}, λ)$ , describes the angular distribution of unpolarized light scattered from its initial direction ${\hat{ξ}}^{'}$ into direction $\hat{ξ}$ at a wavelength $λ$ . If the medium is isotropic, the scattering is azimuthally symmetric about the incident direction. Then the scattering depends only on the angle $ψ$ between the incident ( ${\hat{ξ}}^{'}$ ) and ﬁnal ( $\hat{ξ}$ ) directions. The assumption of azimuthal symmetry is valid for spherical particles or randomly oriented non-spherical particles for unpolarized incident irradiance. This assumption is almost always valid for the turbulent aquatic environment. In this case, the VSF can be deﬁned as the radiant intensity, $d I (ψ, λ) [W s r^{- 1} n m^{- 1}]$ emanating at an angle $ψ$ from an inﬁnitesimal volume element $d V [m^{3}]$ for a given incident irradiance, $E (0, λ) [W m^{2} n m^{- 1}]$ (recall Eq. 2 of The VSF and Eq. 6 of Measuring IOPs):

β (ψ, λ) = \frac{1}{E (0, λ)} \frac{d I (ψ, λ)}{d V} [m^{- 1} s r^{- 1}] .

A measure of the overall magnitude of the scattered light, without regard to its angular distribution, is given by the scattering coeﬃcient, $b (λ) [m^{- 1}]$ , which is the integral of the VSF over all angles ( $4 π s r$ ).:

b \equiv \int_{4 π} β (\hat{ξ}) d Ω (\hat{ξ}) = \int_{0}^{2 π} \int_{0}^{π} β (ψ, ϕ) sin ψ d ψ d ϕ = 2 π \int_{0}^{π} β (ψ) sin ψ d ψ,

where $Ω (\hat{ξ})$ is an element of solid angle centered on direction $\hat{ξ}$ . $ψ$ and $ϕ$ [rad] are the polar and azimuth angles, respectively, centered on ${\hat{ξ}}^{'}$ . For compactness of notation we can drop the $λ$ argument, although it is understood that all the IOPs, unless speciﬁed otherwise, are functions of the wavelength. Scattering is often described by the phase function, which is the VSF normalized to the total scattering. It provides information on the shape of the VSF regardless of the magnitude of the intensity of the scattered light:

\tilde{β} (ψ) \equiv \frac{β (ψ)}{b} .

Other parameters that deﬁne the scattered light include the backscattering coeﬃcient, $b_{b}$ , which is deﬁned as the total light scattered into the hemisphere from which light has originated (i.e., scattered in the backward hemisphere of directions, denoted by $2 π_{b}$ ):

b_{b} \equiv \int_{2 π_{b}} β (\hat{ξ}) d Ω (\hat{ξ}) = 2 π \int_{π ∕ 2}^{π} β (ψ) sin ψ d ψ,

and the backscattering ratio, which is deﬁned as

\tilde{b} \equiv \frac{b_{b}}{b} .

See comments posted for this page and leave your own.

Comments for Scattering Overview:

Loading Conversation

The Physics of Scattering »