Luminosity Functions

If the human eye is the sensor, then all visible wavelengths are seen simultaneously, and monochromatic radiometric variables, IOPs, and AOPs must be replaced by broad-band values that depend on both the wavelength dependence of the ambient radiance and on the relative sensitivity of the eye to diﬀerent wavelengths. This is eﬀected by replacing these quantities by their photopic equivalents.

Not all wavelengths of light evoke the same sensation of brightness in the human eye-brain system. For example, suppose a person with “normal” eyesight is exposed to monochromatic radiance of wavelength 550 nm and magnitude of $1 0^{3} W m^{- 2} s r^{- 1} n m^{- 1}$ . (This is comparable in magnitude to the sun’s spectral radiance at this wavelength when seen through a hazy atmosphere or at a large solar zenith angle.) The person will “se” a bright yellowish-green light. However, if the person is exposed to light of the same radiance magnitude, but of wavelength 300 nm, the person will not “see” anything because the eye is not sensitive to this ultraviolet wavelength. However, if the exposure lasts long enough, permanent and severe damage will be done to the eye by the ultraviolet radiant energy.

The relative ability of radiant energy of diﬀerent wavelengths to evoke diﬀering sensations of brightness in the human observer is described by luminosity functions. The cone cells of the human eye are responsible for color vision at daylight levels of the ambient illumination. These cells have a sensitivity described, when averaged over many individuals, by the photopic luminosity function. The rod cells are responsible for vision in very dim light, such as at night. These cells are more eﬃcient at seeing blue wavelengths and less eﬃcient at red wavelengths than are the cones. The eye sensitivity at low-light conditions is given by the scotopic luminosity function.

The photopic and scotopic luminosity functions are plotted in Fig. 1. These functions are empirically derived averages based on visual response studies of numerous humans. In these studies a colored light is viewed next to a reference light. The observer adjusts the power of the colored light until it subjectively appears to have the same brightness as the reference light. The reciprocal of the measured radiance of the colored light is then plotted at the wavelength of the colored light. This process of “brightness matching” is subjective and there is considerable variance among observers, so the resulting average over many observers has somewhat the same statistical validity as the “average American male, age 30.” Nevertheless, the functions serve as reasonable reference standards for human eye response. Suppose, for example, that monochromatic radiance $L (λ = 500 n m)$ (blue-green light) of some given magnitude (in $W m^{- 2} s r^{- 1} n m^{- 1}$ ) evokes a certain qualitative sensation of brightness in the eye. Then from Figure 1 we see that in order to produce the same sensation of brightness with red light of wavelength 650 nm requires about three times the radiance, i.e. $L (λ = 650) \approx 3 L (λ = 500)$ .

Figure 1: Luminosity functions for bright and dim light. Left panel: normalized funtions; right panel: functions in lumen per watt. (The photopic function is the 1931 CIE 2-degree function in energy units; see www.cvrl.org/lumindex.htm; see also Table 2.1 of Light and Water (1994).)

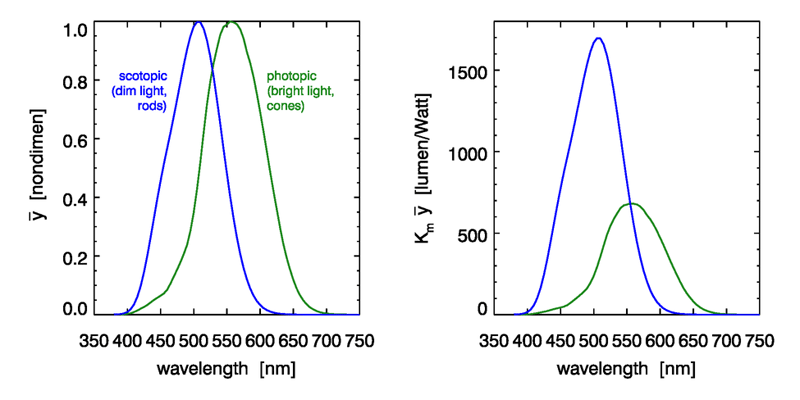
The normalized photopic luminosity function is denoted by $ȳ (λ)$ . The spectral radiance $L (λ)$ , weighted by $ȳ (λ)$ and integrated over all wavelengths (in practice, usually from 380 to 720 nm or even just 400 to 700 nm) gives the luminance $L_{v}$ , which is the photopic, or vision, equivalent of radiance:

L_{v} \equiv K_{m} \int_{0}^{\infty} L (λ) ȳ (λ) d λ [l m m^{- 2} s r^{- 1}] .

(1)

Here $K_{m}$ is a fundamental physical constant called the luminous eﬃcacy that by deﬁnition has the value $K_{m} = 683 l u m e n W^{- 1}$ exactly. (See the Units page. This quantity converts radiance from energy units (Watts or Joules per second) to the visual unit of lumens (abbreviated lm). The numerical value of $K_{m}$ traces back to the idea of the visual brightness of a “standard candle.” The modern deﬁnition of a lumen is that the surface of melting platinum (at a temperature of 2042 K) emits luminance of $6 \times 1 0^{5} l m m^{- 2} s r^{- 1}$ . The luminance $L_{v}$ corresponds to the visual impression of brightness. The subscript $v$ (for visual) on a radiometric quantity ﬂags it as the corresponding photometric quantity.

As seen in the units of $K_{m}$ , the lumen is the visual correspondent of radiometric power in watts. The SI base unit for photometric variables in the candela, abbreviated cd. The deﬁnition of the candela is “The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency $540 \times 1 0^{12}$ hertz and that has a radiant intensity in that direction of 1/683 watt per steradian.” (This frequency corresponds to $λ = 555 n m$ for light in a vacuum.) Recall that radiometric intensity is power per unit solid angle. The candela is correspondingly luminous power per unit solid angle, i.e. $1 c d = 1 l m, s r^{- 1}$ . The lumen is then a derived quantity, which by deﬁnition is $1 l m \equiv 1 c d s r$ . Unsuccessful attempts have been made to have the lumen adopted as the SI base unit; the proposed deﬁnition being “the lumen is the luminous power of monochromatic radiant energy whose radiant power is 1/683 W and whose frequency is $540 \times 1 0^{12} H z$ .” Neither of these deﬁnitions is particularly enlightening, so for intuitive purposes, think of an ordinary candle as having a luminous intensity of about 1 cd, or $1 l m s r^{- 1}$ . The candela (Latin for candle) indeed traces back to the historical use of a “standard candle” as the unit of brightness. (One of the historical deﬁnitions of a standard candle was the “light produced by a pure spermaceti candle weighing one sixth of a pound and burning at a rate of 120 grains per hour.”)

For conversion of night-time, or dim-light, radiances to luminance, an equation of the same form as (1) is used but with the scotopic luminosity function, denoted $ȳ^{'} (λ)$ . The conversion factor for the scotopic luminosity function is $K_{m}^{'} = 1700 l m W^{- 1}$ . Thus the rods are more eﬃcient at converting radiant energy into visible light, but at the tradeoﬀ of giving only gray-scale images.

As an example, we can compute the luminance of the sun. The Sun’s output can be approximated as that of a blackbody at a temperature of $T = 5782 K$ . The radiance of a blackbody is given by Eq. (6) on the blackbody radiation page:

L_{B B} (λ) = \frac{2 h c^{2}}{λ^{5}} \frac{1}{e^{h c ∕ λ k T} - 1} .

(2)

Using this radiance in Eq. (1) gives

L_{v}^{s u n} = K_{m} \int_{0}^{\infty} L_{B B} (T = 5782 K, λ) ȳ (λ) d λ = 1.86 \times 1 0^{9} l m m^{- 2} s r^{- 1} .

This is the value in the ﬁrst line of Table 1.


Source	Luminance
.	$(l m m^{- 2} s r^{- 1} = c d m^{- 2})$

solar disk, above the atmosphere	$2 \times 1 0^{9}$
solar disk, at Earth’s surface, Sun near the zenith	$1 \times 1 0^{9}$
melting platinum at 2042 K	$\equiv 6 \times 1 0^{5}$
60 W frosted light bulb	$1 \times 1 0^{5}$
sunlit snow surface	$1 \times 1 0^{4}$
full Moon’s disk	$6 \times 1 0^{3}$
clear blue sky, directions away from the Sun	$3 \times 1 0^{3}$
heavy overcast, zenith direction	$1 \times 1 0^{3}$
twilight sky	$3$
clear sky, moonlit night	$3 \times 1 0^{- 2}$
overcast sky, moonless night	$3 \times 1 0^{- 5}$

Table 1: Typical luminances.

All radiometric quantities have a photometric equivalent obtained by an equation of the form of (1). Thus the photometric equivalent of the downwelling plane irradiance $E_{d} (λ)$ , which is called the downwelling plane illuminance, is given by

E_{d v} \equiv K_{m} \int_{0}^{\infty} E_{d} (λ) ȳ (λ) d λ [l m m^{- 2}],

and so on. Just as irradiances can be computed from radiances, illuminances can be computed from luminances by equations of the same form as for radiometric variables. For example,

E_{d v} = \int_{2 π_{d}} L_{v} (𝜃, ϕ) | cos 𝜃 | sin 𝜃 d 𝜃 d ϕ .

Table 2 shows typical illuminances $E_{d v}$ . In illumination engineering, one lumen per square meter is called a “lux.” Thus the instruments used to measure brightness is rooms are often called lux meters (photographers usually call them light meters).


Source	Iluminance
.	$(l m m^{- 2} = l u x)$

Sun at the zenith, clear sky	$1 \times 1 0^{5}$
Sun at 60 deg zenith angle, clear sky	$5 \times 1 0^{4}$
overcast day	1000
well-lit room	300-500
very dark, heavily overcast day	100
full Moon at 60 deg zenith angle, clear sky	0.2
starlight, moonless night, clear sky	$4 \times 1 0^{- 3}$
moonless night, heavy overcast, in a thick forest	$1 0^{- 4}$

Table 2: Typical Illuminances

E_{d v}

Photometric equivalents of apparent optical properties are obtained from the photometric variables just as AOPs are obtained from radiometric variables. Thus the illuminance reﬂectance is given by

R_{v} = \frac{E_{u v}}{E_{d v}},

the photometric diﬀuse attenuation function for $E_{d v}$ is given by

K_{d v} (z) = - \frac{d ln E_{d v} (z)}{d z},

and so on.

Luminosity Functions

Comments for Luminosity Functions: