Page updated:
May 25, 2021
Author: Curtis Mobley
View PDF
Lambertian BRDFs
Actual measurements of BRDFs of ocean bottom materials like sand or sea grass canopies have rarely been made, although some measurements of sediments do exist (e.g., Zhang et al. (2003)). Because of the lack of measurements and models of the BRDF for actual ocean bottom materials, it is usually assumed that a bottom is a Lambertian reflecting surface.
A Lambertian surface by definition reflects radiance equally into all directions. Its BRDF is simply
| (1) |
where is called the reflectivity of the surface. The reflectivity varies from zero for a completely absorbing (“black”) surface, to one for a completely reflecting (“white”) surface. There are no Lambertian surfaces in nature, but matte paper is good approximation except at grazing angles and near 90 degrees), where the surface begins to look “shiny.”
There is sometimes confusion as to how Lambertian surfaces reflect light. You will sometimes see a statement like
- A Lambertian surface reflects light equally into all directions. Lambertian surfaces therefore are also called isotropic/uniform/perfectly diffuse reflectors.
You can also see statements like
- A Lambertian surface reflects light with a cosine angular distribution. Lambertian surfaces therefore are also called cosine reflectors.
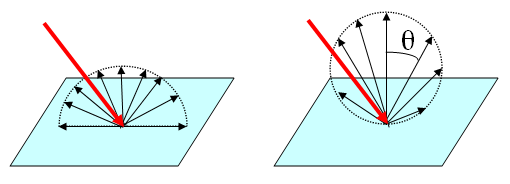
These statements conjure up different mental images, as shown in Fig. 1, and appear to be contradictory.
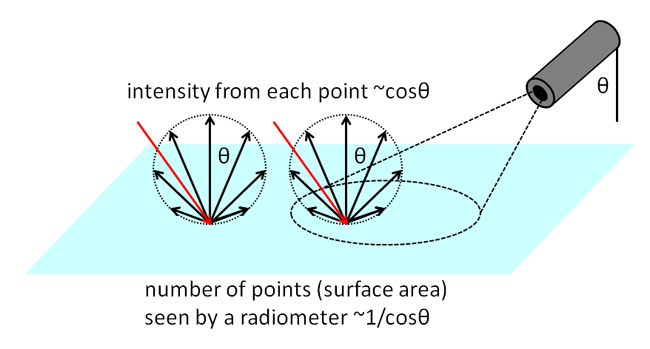
However, either statement can be correct or incorrect, depending on which measure of light is used. Each point of a Lambertian surface reflects intensity in a cosine pattern, as in the right-hand panel of Fig. 1, which is the correct form of the second statement. However, when the surface is viewed with a radiometer with a finite field of view, the area of the surface seen by the radiometer is proportional to . The radiance measured comes from the the intensity reflected from each point times the number of points seen , and is therefore independent of . Thus the measured reflected radiance is independent of the viewing direction, which corresponds to the first statement. This is illustrated in Fig. 2.
In addition to their mathematical simplicity, Lambertian surfaces have an extremely important property. To see what it is, compute the irradiance reflectance of a Lambertian surface (here we use d and u subscripts to identify the downwelling and upwelling irradiances, respectively, as is common in optical oceanography, but we’ll keep the i and r subscripts in the integrals):
The first equation here is just the definitions of the plane irradiances in terms of the incident (downwelling) and reflected (upwelling) radiances. The differential of solid angle is , and the double integrals are over the corresponding hemispheres of . In going to the second equation, Eq. (3) of the BRDF page has been used to write the upwelling radiance reflected from the surface in terms of the downwelling radiance onto the surface and the BRDF of the surface. Equation (2) is completely general and is the fundamental equation for computing the irradiance reflectance of any surface, given the BRDF of the surface and the incident radiance onto the surface.
Substituting the Lambertian BRDF of Eq. (1) into Eq. (2) and rearranging gives
since the integrals over cancel, and the integral over equals . A Lambertian surface thus has the property that its irradiance reflectance equals its reflectivity and, furthermore, its irradiance reflectance is independent of the incident radiance. Both of these results are true only for Lambertian surfaces. For non-Lambertian surfaces, generally depends both on the surface and on the incident lighting, as seen in Eq. (2).
Fortunately, the use of a Lambertian BRDF for ocean bottom materials in radiative transfer calculations usually results in errors of less than 10 per cent (and often less) in predicted upwelling radiances as viewed for near-nadir directions (the geometry for most remote sensing), so long as the reflectivity of the assumed Lambertian surface equals the irradiance reflectance of the actual non-Lambertian surface. Thus the crucial measurement to make is the irradiance reflectance of the bottom for the incident lighting conditions of interest (Mobley et al., 2003).

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.