Page updated:
November 2, 2020
Author: Curtis Mobley
View PDF
The Henyey-Greenstein Phase Function
It is often convenient to have an analytic formula that approximates the shape of an actual phase function. The Henyey-Greenstein (HG) phase function has been widely used in the past for such purposes and is discussed here for historical completeness. The Henyey-Greenstein phase function (and many other simple analytical models) has now been supplanted in oceanography by the more complicated but more realistic Fournier-Forand phase function.
Henyey and Greenstein (1941) proposed the phase function
| (1) |
for scattering by interstellar dust (note: interstellar dust, not phytoplankton!). The parameter can be adjusted to control the relative amounts of forward and backward scattering in : corresponds to isotropic scattering, and gives highly peaked forward scattering. Note that satisfies the normalization condition
The physical interpretation of comes from noting that
Thus the Henyey-Greenstein parameter is just the average of the cosine of the scattering angle for .
Equation (1) can be integrated over from to to obtain the backscatter fraction:
Because of its mathematical simplicity, the HG phase function has been widely used in many fields, including oceanography. However, we can anticipate discrepancies between and measured oceanic phase functions because oceanic particles are quite different in their physical properties (size, shape, composition from interstellar dust.
The average of for the Petzold average-particle phase function is 0.924. Using in Eq. (1) thus gives the Henyey-Greenstein phase function corresponding to the particle phase function , in the sense that each phase function then has the same average cosine. Figures 1 and 2 compare and . is also shown for and 0.99. Note that the best-fit differs noticeably from at scattering angles greater than and less than 20 deg, and that is much too small at angles of less than a few degrees. The small-angle behavior of Eq. (1) is inherently incompatible with because always levels off as , whereas continues to rise. Even for , is nearly constant for . For , , compared to the backscatter fraction of 0.0183 for the Petzold phase function.
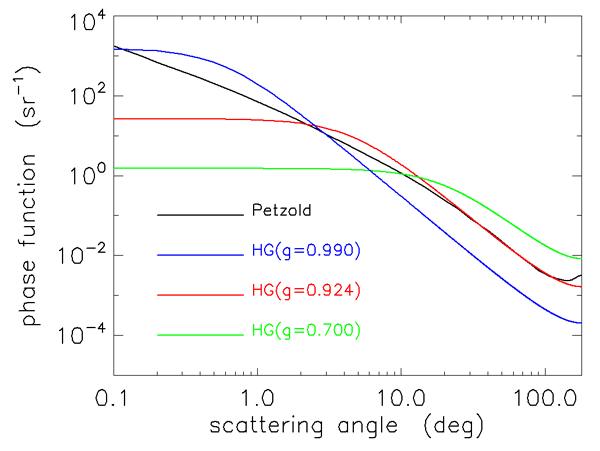
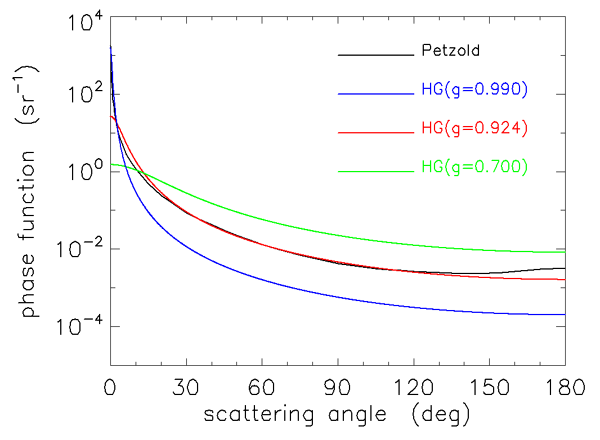
Because of the poor fits of the HG phase function to measurements at small and large scattering angles, a linear combination of Henyey-Greenstein phase functions is sometimes used to improve the fit at small and large angles. The so-called two-term Henyey-Greenstein (TTHG) phase function is
| (2) |
Enhanced small-angle scattering is obtained by choosing near one, and enhanced backscatter is obtained by making negative; is a weighting factor between zero and one. Kattawar (1975) shows how to determine best-fit values of , , and for a given phase function. Reasonable fits can be obtained with the TTHG function for phase functions that are not highly peaked, for example atmospheric haze phase functions (see Kattawar’s paper for example fits). However, the fit of to highly peaked oceanic phase functions such as always remains unsatisfactory at very small angles, for the reason already noted.

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.